在阮一峰的博客上发现一篇有意思的推荐文章,讲述了椭圆曲线加密算法(Elliptic Curve Cryptography)的实现原理,原作者友好的将文章使用的源代码放在了Github供读者使用,我也成功在Ubuntu搭建起了实验环境。此文的原意并不是深究ECC算法是如何实现安全地加密,而是让感兴趣的读者可以易于理解ECC算法的基本逻辑,我也不是密码学方面的专家,所以文章不严谨的地方烦请斧正。
We also don’t want to dig too deep into the mathematical rabbit hole
首先,我们有一个二元三次方程组。
$$
y^2=x^3+ax+b
$$
在假设a=-1,b=5的情况下,我们可以得到如下图的曲线:
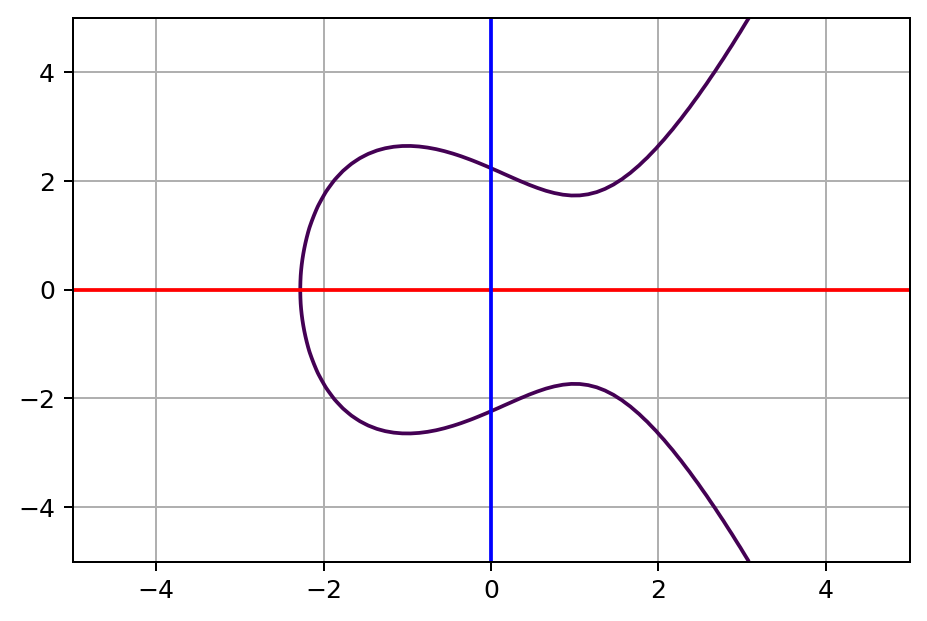
然后,我们随机选取两个X的值,那么我们就可以通过计算Y值得出蓝色的A和蓝色的B两个坐标。下一步,我们把蓝色的A和B两点连接,他们的连接线将会与曲线在一点相交,我们把这个相交点的Y值反转,即可得到如下图所示的橙色A+B点。这里留一个疑问,蓝色A点+蓝色B点的值会等于橙色A+B点吗?
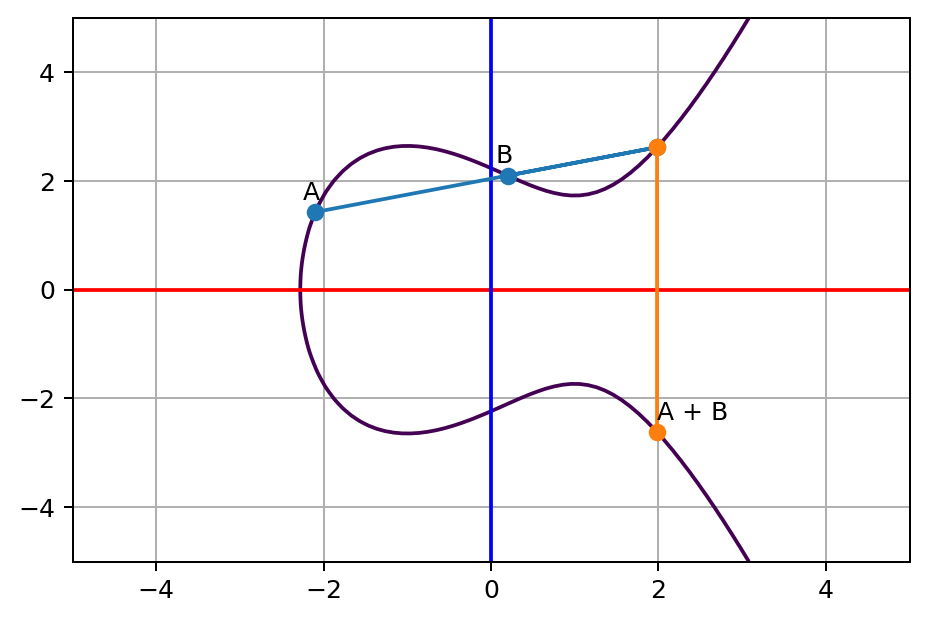
紧接着,我们把A+B点连接到曲线上的某一点C。同样的,只要这一条线不是垂直的,我们就可以在A+B点和C点之间的连接线中找到一个与曲线相交的点,我们一样把这个相交点的Y值反转,即可得到如下图所示的橙色A+B+C点。
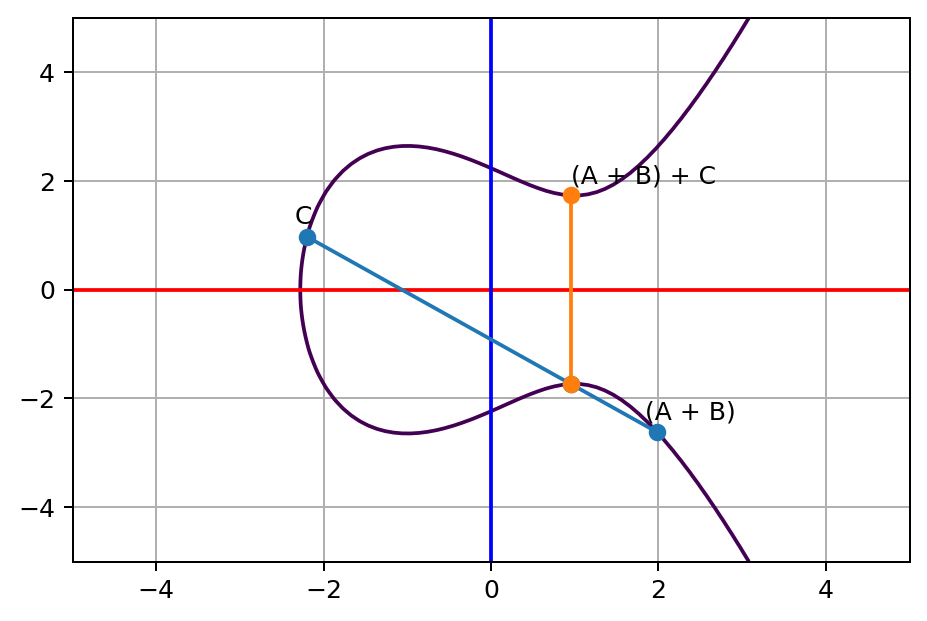
如此类推,我们就可以不断的通过这样的方法,从一点出发得到另外一个新的点。为了便于更直观的理解,我们希望用相同的点P来表示每一个新的点,所以我们利用当前位置的切线来得到点P,用同样的办法得出P+P点(或称2P点),得到如下图:
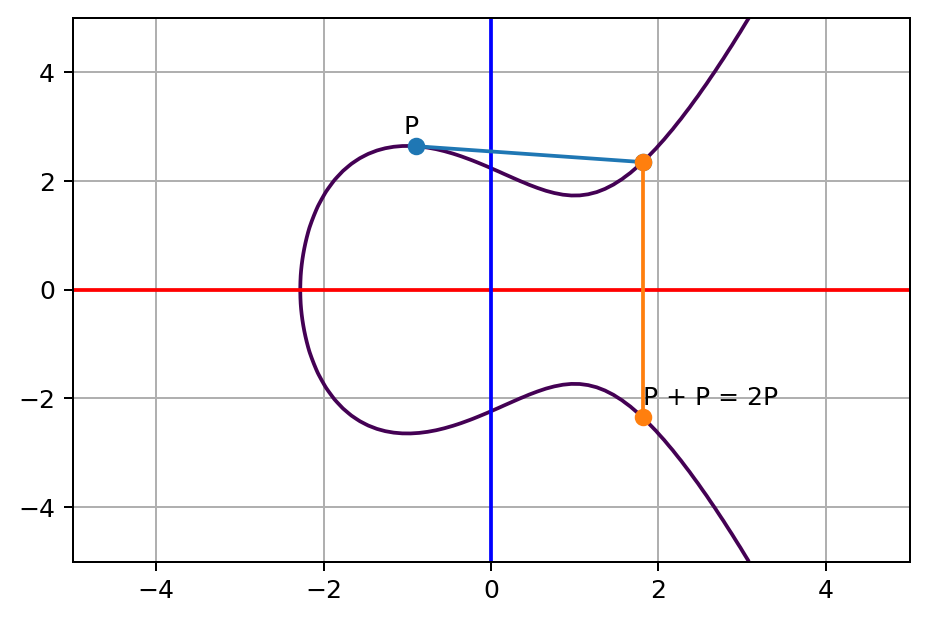
接下来,我们再一次从P+P点回到原始的P点,得到的结果,我们称之为P+2P+3P(或称3P点)
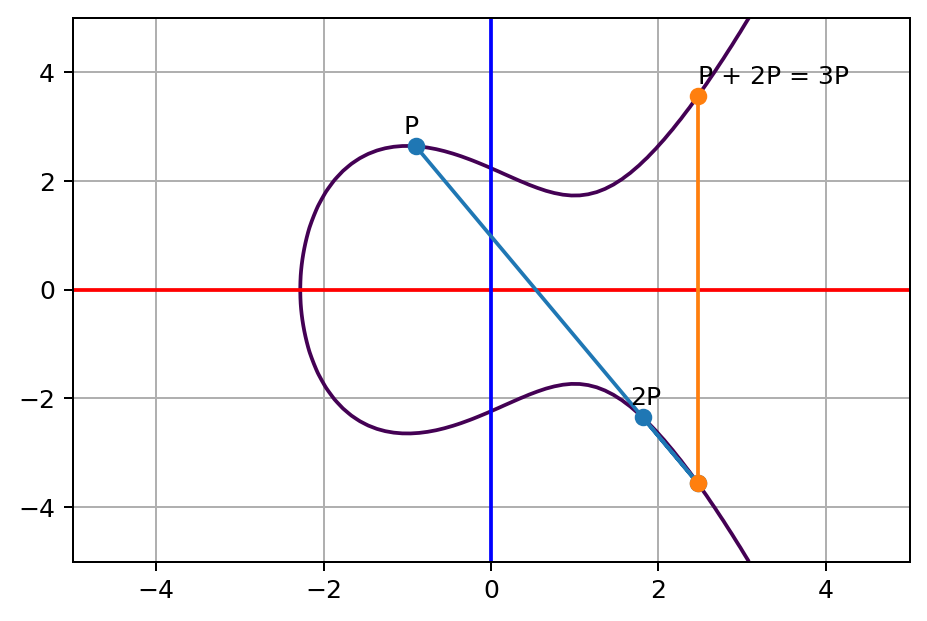
类似的,我们可以利用这个方法一直持续下去N次,得到NP。那么当我只告诉你如下图的NP的坐标(意味你已知NP)时,你可以不可以推算出N的次数呢?
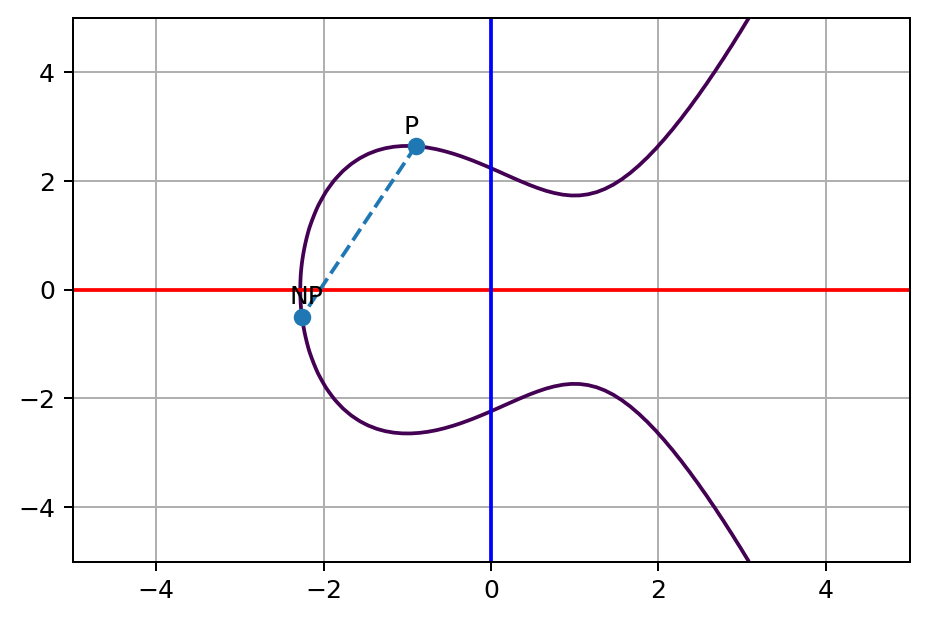
这里N=13,因为图是作者画的,所以她肯定知道呀。但如果排除这种情况以外(已得知N值),你将很难通过推算找到答案。听到这里,大概密码学的味道开始出现了,N代表的就是私钥,而NP代表的就是公钥。换句话说就是,当我们知道NP和P的值的时候,推算出N的值是困难的。
有人就会问了,当我已经知道NP和P的值,那么我可以从P+P开始,再到P+2P+3P的一直尝试下去,不就可以得到NP了吗?那我们接下去看。首先我们看到下面的加法交换律,
$$
a+(b+c)=(a+b)+c
$$
我们可以借助作者提供的源码,在 jupyter notebook 中计算出坐标点A,点B和点C不同顺序相加的结果:
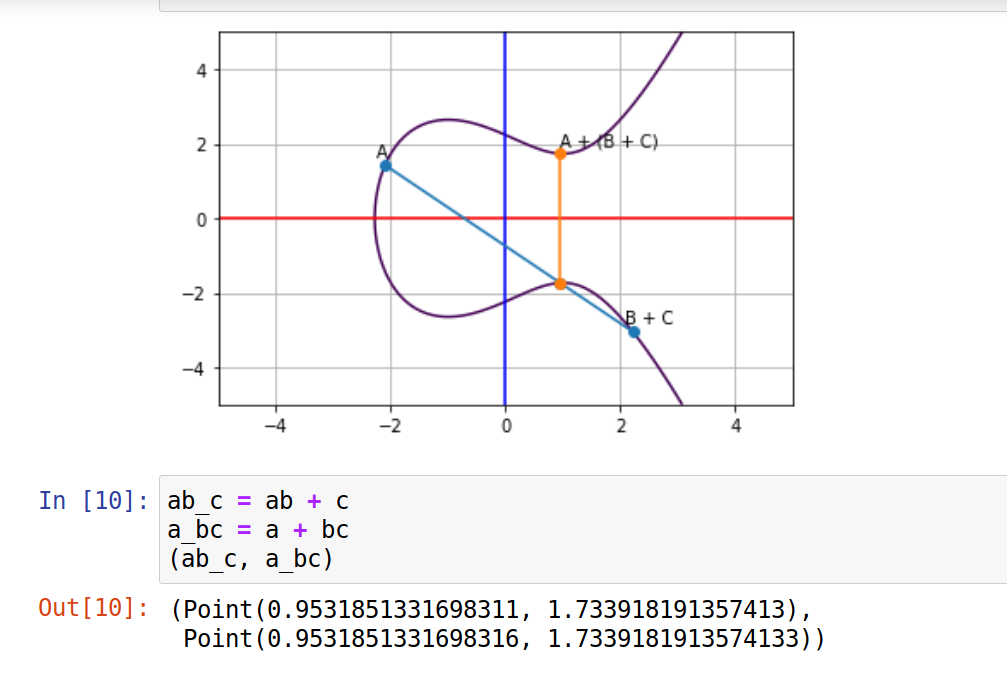
两者的结果是非常接近的,造成误差是由于算法的浮点类型设置,另外原文也已经解释了关于数学有限域的问题,但这不是本文着重点。这里我们认为加法交换律是成立,得出结论一:坐标点可以无序的相加而不影响结果。
刚刚“加法交换“的例子我们已经讲到(已知)P+2P=3P,那么下面式子是不是成立呢?
$$
P+3P=4P=2P+2P
$$
同样在电脑上使用 jupyter notebook 计算一次,我们得出下面的两个图:
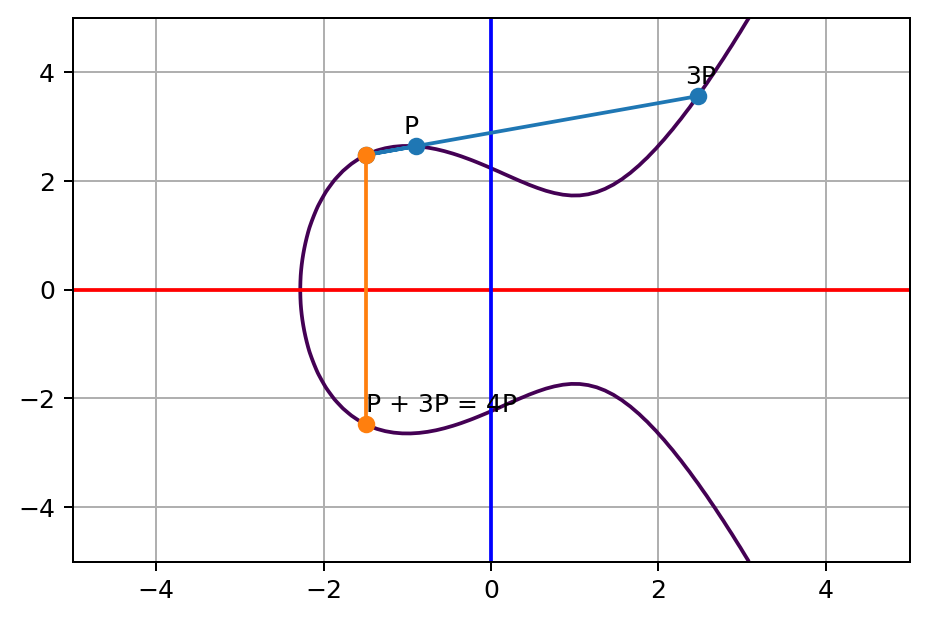
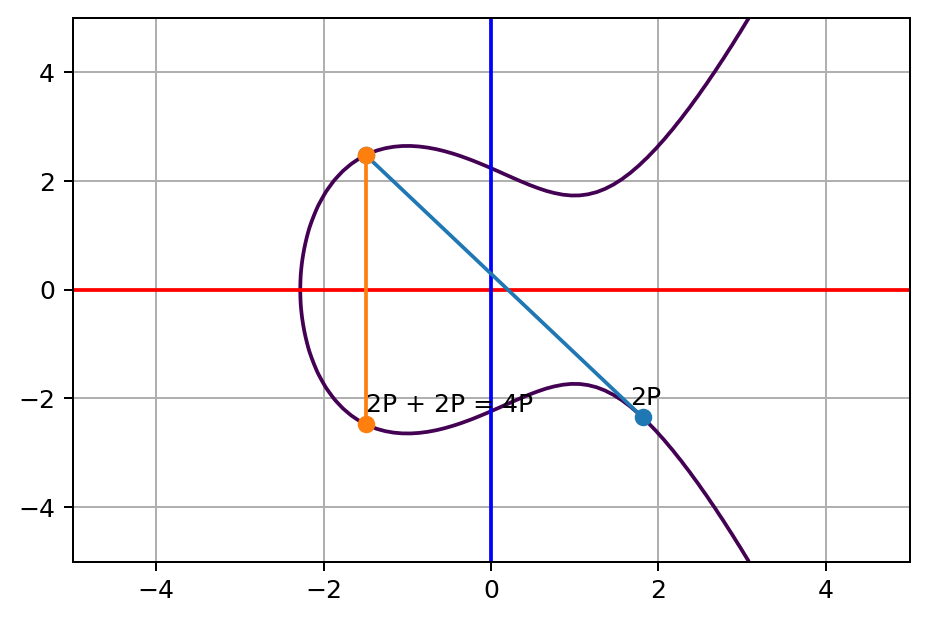
等式两边的结果都是在同一个点上,即上面的式子是成立的,得出结论二:将坐标点化作成倍关系的累加是不影响结果的。有了上面两个结论,我们就可以开外挂来“加速运算”了,所以回到刚刚的问题:
我可以从P+P开始,再到P+2P+3P的一直尝试下去,不就可以得到NP了吗?
举个例子,已知N=227,尝试分解227P的运算过程。首先将227分解成用二进制的方式表达:
$$
11100011
$$
接着代入P点的坐标,且将二进制运算转换为对应的幂运算,式子如下:
$$
2^7P+2^6P+2^5P+2^1P+2^0P
$$
等同于:
$$
128P+64P+32P+2P+P
$$
相比于逐次累加227次运算得出227P的结果,上面的式子可以化简为8次运算就可以得出结果,也比较符合计算机的运算方式。因此,对于猜解N值,幂运算的方法比逐次累加的方法快太多了。接下来就是熟悉的同底数幂相加和求对数的问题,例如:
$$
a^x+a^y=a^{x+y}
$$
$$
3^4 = 3\times 3\times 3\times 3=81
$$
$$
4=log_381
$$
所以求解N的值就可以转换成对数的求解。那为什么已知NP求解N是困难的?因为椭圆曲线密码体制就是建立在对椭圆曲线离散对数问题(ECDLP)求解困难性假设基础上 ,如开头所说的,本文不深究数学问题。只需要知道当N值变成更大的数字,例如 2256 或者 1082 的时候,攻击者逐次累计的方式就变得无效,且保证了攻击者在已知NP和P的情况下,无法计算出N值。
Namely, find out what’s the N value from NP and P point given if N is big enough. This is called Elliptic Curve Discrete Logarithm Problem.
文章最后举例Alice和Bob是如何交换密钥以及实现加密通信的。
第一步,约定使用ECC算法作为加密协议;
第二步,Alice发送公钥P和NP值给Bob,N为Alice的私钥。当N值足够大的时候,已知NP来求解N是困难的,因此N值只有Alice知道;
第三步,Bob同意使用公钥P,并且回复MP给Alice,M为Bob的私钥。当M值足够大的时候,已知MP来求解M是困难的,因此M值只有Bob知道;
第四步,协商一个对称加密算法,如AES256。Alice和Bob使用共享的密钥SK来加密和解密信息;
$$
SK=NP\times M=MP \times N
$$
这里又有一个新的安全问题,那就是Alice如何校验MP这个值就是来自Bob的呢?因此需要引入公钥基础设施(Public key infrastructure)的概念来防止中间人攻击(MITM attack),例如HTTPS绿锁头的原理。
参考资料:
Elliptic Curve Cryptography Explained
How To Set Up Jupyter Notebook with Python 3 on Ubuntu 18.04 | DigitalOcean